"Mathematics with Maple"

S.Duzhin

Lesson 1: First acquaintance with Maple

This is a Maple worksheet. It is an "alive" lesson, because it contains not only usual text which you can read, but also command text that can be interpreted by computer.

Command lines are printed in red and have a special character ("prompt") at the beginning. When you put the cursor into a command line and press "enter", Maple will begin computing and after some time give an answer.

Let us try it now. Put the cursor into the following line and press "enter":

> 2+2;

In the previous line, right in the middle, the answer has appeared.

After completing a command, the cursor jumps to the next red line, so that sometimes you will have to bring it back -- either with your mouse or with the arrow keys. Try it now!

Main rules for a Maple beginner.

1. Any command should end by a semicolon (;) and "enter".

Corollary: a command may occupy several lines.

Example:

> 1+2+3+

> 4+5+6;

2. To quit Maple, type "quit" or choose "exit" from "file" menu. If you want to try it now, you will have to start Maple once again. Ready? Come on!

> quit;

3. If you forget the name or usage of some Maple command, go ahead and use the on-line help.

To access help, you can write a question mark (?) followed by any word or part of a word. For example, if you forgot the word "differentiate", but you remember that it begins with "dif", write:

> ?dif;

It works fine --- only the explanation given is in English, which may cause problems!

Fortunately, the texts you have to read are usually quite simple.

So, let us try one of the words suggested:

> ?differentiate;

I hope you have managed to return from the help window that suddenly opens up. (In these cases, a simple rule is useful: try to find "exit" or "quit" in the "file" menu).

From the examples given in the help window, it is easy to understand the format of the differentiation operator: diff(f(x),x). Shall we try it?

> diff(sin(x),x);

Another useful way to get on-line help is through menu item "help" which is an entry point into the complete tree of Maple help. You will be able to see it later yourselves, but now we will go on with the lesson.

The main features of Maple system are:

1. Numeric computations

2. Symbolic computations

3. Graphics

4. Programming

Now we will look at some examples related to each of these items.

As soon as you see a red line, you can put the cursor in it and press "enter".

Let us warm up by computing 200! = 1*2*3*...*200.

> 200!;

The answer occupies several lines, and backslashes (\) are continuation signs.

One more example of integer arithmetic: factorization of integers into prime numbers:

> ifactor(2^32+1);

This was a famous number in the history of mathematics. In 17th century P.Fermat conjectured that it is prime, and everybody thought so until about 100 years later, when L.Euler found the decomposition which Maple can find in a fraction of a second.

Now let us see whether Maple can work with irrational numbers. The problem we will give is to find the square root of 2:

> sqrt(2);

Has Maple solved this problem or not? What do you think?

The answer seems to be 'no', but in fact the solution given by Maple only means that it understands the nature of irrational numbers and knows that there is no simpler way to write down the exact value of sqrt(2). We can check it like this:

> sqrt(2)*sqrt(2);

If you want to find a decimal approximation to this number, you can use the Maple function evalf ('floating evaluation' -- you know the word 'floating' from your C programming classes):

> evalf(sqrt(2));

To find the value of sqrt(2) to 100 digits, issue the command

> evalf(sqrt(2),100);

Maple knows the famous mathematical constants E and Pi:

> exp(1);

> Pi;

Here are their approximate values:

> evalf(exp(1));

> evalf(Pi);

Now some examples of symbolic computations -- work with algebraic formulas.

First we write an expression in its initial form, then, in the next line, apply one of the symbolic procedures of Maple. The percent sign (%) means 'the result of previous computation'.

The first operation is expansion (removal of brackets):

> (x+y)^3*(x-y)^3;

> expand(%);

> sin(x+y);

> expand(%);

Factorization (rewriting an expression as a product of two or more simpler expressions):

> x^3+y^3+z^3-3*x*y*z;

> factor(%);

Finding the common denominator:

> (x-y)/(x+y)+(y-z)/(y+z)+(z-x)/(z+x);

> normal(%);

Differentiation (finding the derivative of a function):

> f:=x^x;

> diff(f,x);

Indefinite integration:

> f:=x/(x^2+x+1);

> int(f,x);

You may notice that Maple is quite good at finding indefinite integrals (it could help you a lot during the written test in calculus last year!)

It can also compute definite integrals. Here is an example of finding the numerical value of a definite integral:

> evalf(int(E^sin(x),x=0..1));

Now let us try some examples related to solution of equations -- both symbolic and numeric. To solve one equation, you simply write solve(equation,unknown).

If the equation is solvable by radicals (i.e. its solution can be written in terms of the 4 operations of arithmetic and root extraction), then Maple usually is able to find this solution exactly, for example:

> solve(x^2+x-5=0,x);

If the equation is not solvable by radicals, the answer given by Maple looks something like this:

> solve(x^5+2*x=1,x);

In such a case an approximate solution can be found with the help of 'evalf' (this does not guarantee that ALL roots are found; we will discuss this problem later):

> evalf(%);

Here the big letter I is the Maple notation for the imaginary unit sqrt(-1).

OK. Enough with computations for today. Let us draw some pictures.

First we will prepare a nice example:

> p:=cos(7*arccos(x));

> expand(%);

It is surprising that all trigonometry disappeared, and we are left with a polynomial expression!

Now let us draw the graph of this function, and you will see that the example is really very nice (it is called "Chebyshev polynomial of degree 7").

> plot(%,x=-1..1);

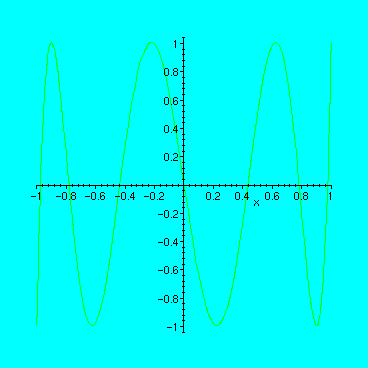
In the graphics window where the picture appears, there is a menu which gives you possibility to change the character of the plot.

However, this menu is much more interesting for 3-dimensional plots, so let us wait until the next example.

The next (and the last in this lesson) example is the graph of a function of two variables z=f(x,y). This graph is a surface in 3-dimensional space, and it usually takes some time for the computer to complete the plot.

When the plot is ready, go head and use your mouse (1) to rotate it in space, and (2) to choose various options for the style, colors and projection.

> plot3d(cos(x)+cos(y)+cos(x+y),x=0..2*Pi,y=0..2*Pi);

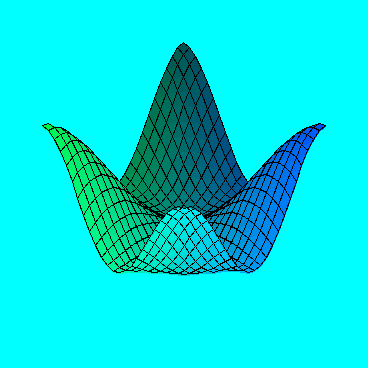
This is the end of today's examples. In this first review of Maple, we have covered some numerics, symbolics and graphics. We will talk about Maple programming in a separate lesson. We will also study some simple, but interesting mathematics with the help of Maple.

A final remark: if you want to print this worksheet (or any Maple document), choose "print" in the "file" menu.

Exercises:

1. Go through this worksheet once again and give your own examples for the commands:
ifactor, evalf, expand, factor, normal, diff, int, solve, plot, plot3d.
(Use Ctrl-J to make empty space for the new command right below the cursor line.)

2. Which of the two numbers is bigger: 1000! or 2^8000 ?

3. Draw the graphs of the two functions f(x)=log[1/16](x) and g(x)=(1/16)^x.

Find all roots of the equation f(x)=g(x).

4. Find a whole number which is not prime but which cannot be factorized by Maple's command ifactor in 1 minute. Try to make this number as small as possible: whoever finds the smallest number with this property will be the winner of this competition.