"Mathematics with Maple"

S.Duzhin

Lesson 3. Solving Equations

Mathematics: polynomials, equations, roots.

Maple: solve, fsolve, plot.

In this lesson, we will study how to solve equations and systems of equations using Maple functions solve, fsolve and plot.

Attention: if you are asked to "find all solutions", this means all "roots", but not all "methods of solution", because it is impossible to find all methods of solution even for the simplest equation!

Because of this misunderstanding, I have not received any correct answers to Exercise 3 from Lesson 1, so let us try to solve it together.

The exercise was:

3. Find all three solutions of the equation log[1/16](x)=(1/16)^x.

Draw the graphs of these two functions.

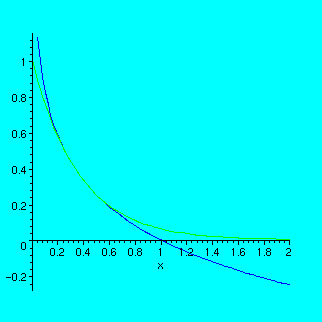
To see what's going on, let us first draw the graphs of these two functions.

You remember how to plot one function:

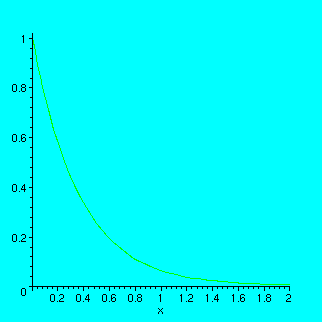
> plot(log[1/16](x),x=0..2);

and

> plot((1/16)^x,x=0..2);

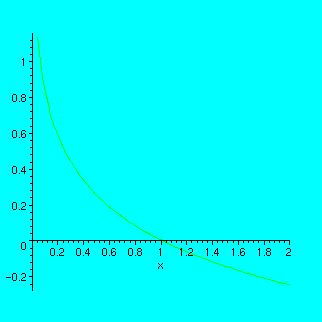
However, if you want to find the roots of an equation like f(x)=g(x), you have to plot two functions together. This can be done using curly braces {}:

> plot({log[1/16](x),(1/16)^x},x=0..2);

{log[1/16](x),(1/16)^x} means the _set_ consisting of two expressions, log[1/16](x) and (1/16)^x.

In the picture that you see, the two graphs are so close to each other on the segment from 0.2 to 0.6 that it is difficult to say how many intersection points are there. There are several ways to cope with this difficulty.

One method is to draw the graphs of the two functions on smaller intervals:

> plot({log[1/16](x),(1/16)^x},x=0.2..0.4);

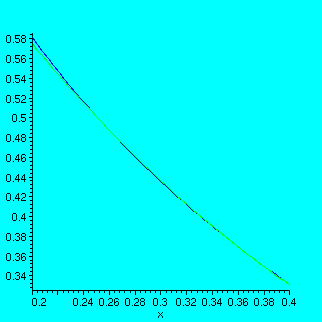
No, this is not enough: you cannot see well. Let us try a smaller interval:

> plot({log[1/16](x),(1/16)^x},x=0.2..0.3);

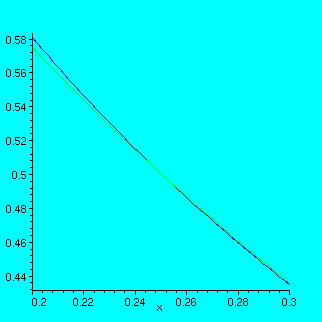
It became more clear now. Let us see the most important piece of this interval with more zoom:

> plot({log[1/16](x),(1/16)^x},x=0.23..0.27);

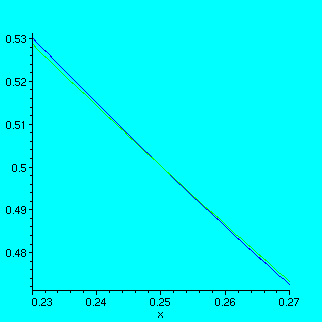
Now it is more or less clear that there is an intersection at 0.25.

Of course, we cannot say that this is exact, but we can check:

> log[1/16](0.25)-(1/16)^0.25;

The answer is so close to 0 that it probably is equal to 0. But, since 0.25 is a floating number, Maple performs approximate computations with it. Shall we try to repeat the same computation with the exact rational number 1/4?

> log[1/16](1/4)-(1/16)^(1/4);

This is a little strange, isn't it? Maple did not try to recall the properties of logarithm and exponents when it was solving this example. But we can force it to do so:

> simplify(%);

Now we see that the solution x=1/4 is exact. (Of course, we could also check this without the computer, because log[1/16](1/4)=-1/2 and (1/16)^(1/4)=-1/2).

So, we have found one solution, or one root, of the equation

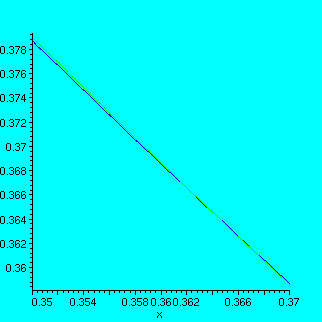
Now you can move along the x-axis and plot the two functions on small intervals, trying to see the intersection points. You will find two intervals containing the roots:

> plot({log[1/16](x),(1/16)^x},x=0.35..0.37);

> plot({log[1/16](x),(1/16)^x},x=0.45..0.55);

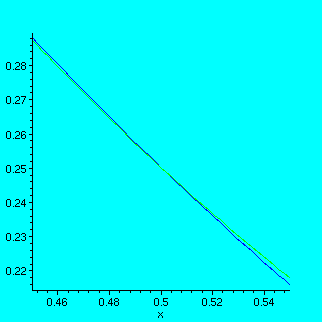
So it looks that our equation has 3 roots, or in other words, 3 different solutions: x=1/4, x ~=0.36 and x=1/2.

But this was a very long procedure to look for the roots.

Fortunately, there is a much shorter way to see all three roots at once: to plot the _difference_ of the two functions on the interesting interval:

> plot(log[1/16](x)-(1/16)^x,x=0.2..0.6);

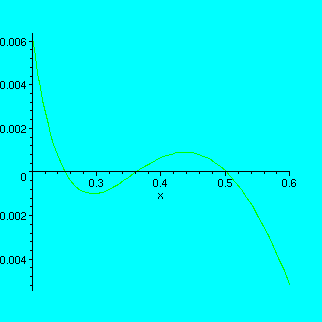
Because the functions are smooth (differentiable), the difference between them near the roots is very small, and you can see it very clearly in the picture. This picture shows that there is one root around 0.25, one root between 0.3 and 0.4, and one root around 0.5.

You can check that 1/4 and 1/2 are exact roots:

> log[1/16](1/2)-(1/16)^(1/2);

> simplify(%);

so it remains to find the approximate solution in the interval 0.3..0.4:

> fsolve(log[1/16](x)=(1/16)^x,x=0.3..0.4);

Thus, the recommended procedure to solve algebraic equations with Maple is as follows:

1. Try function solve. If the equation is simple enough, you will get a complete answer.

2. Draw the graph of the function on several intervals and try to understand the general behaviour of the function. (Here, you also have to use your theoretical knowledge, e.g. that exp(x) grows to infinity when x --> infinity, etc.)

If the equation is of the form f(x)=g(x), try to draw the graph of f(x)-g(x).

3. If necessary, draw the graphs on smaller intervals near suspicious points.

4. Find the intervals [a1,b1], a2,b2],...,[an,bn] that contain 1 root each and use the function fsolve(equation, x=a1..b1) to find the approximate solution in each interval.

Use this procedure to solve the equations given below in Exercises 2-6.

Exercises

1. Plot three functions, sin(x), sin(x+2/3*Pi) and sin(x+4/3*Pi), on the same figure.

2. Solve 16*x^5-20*x^3+5*x=1

3. Solve 32*x^6-48*x^4+18*x^2=1

4. Solve x-x^3/6+x^5/120=0

5. Find all solutions of the equation s in(x)=x-x^3/6.

6. Find the root of the equation x-x^3/6+x^5/120-x^7/5040+x^9/9!-x^11/11!+x^13/13!=0 in the interval (3..3.5)

7. How many solutions does the following system have depending on the parameter a:

x^2+y^2=1, x+y=a.

Hint: draw the graphs of the two equations in the (x,y)-plane using the function implicitplot. Solve the system for a=0, a=0.5, a=1, a=2. Guess the answer. Prove it.

8. The following:

q:=(x-b)*(x-c)/((a-b)*(a-c))+(x-a)*(x-c)/((b-a)*(b-c))+(x-a)*(x-b)/((c-a)*(c-b))-1;

is a quadratic polynomial in x, and equation {q=0} is a quadratic equation. If you put x:=a, or x:=b, or x:=c, you will have q=0. So, we have a quadratic equation that has 3 roots. How is it possible?

9. Make up an arbitrary equation and send it to somebody from your group by e-mail.

He (she) must solve it with Maple.