Mathematics with Maple

S.Duzhin

Lesson 5: Integral

Mathematics: definite and indefinite integral.

Maple: int.

In the previous lesson, we have recalled the notion of derivative and worked with the Maple function diff.

Today, we will review the inverse operation, the integral.

Consider two operations:

1. Differentiation (D):

f --> diff(f,x)

2. Indefinite integration (I)

f --> int(f,x)

Operation I is inverse to D in the following sense.

D(I(f)) = f.

Let us check this on some examples:

> f:=x*sin(x);

> f1:=int(f,x);

> f2:=diff(f1,x);

You see that applying first I, then D, you always get the initial function f:

D(I(f))=f.

What about the reverse order: I(D(f)) = ?

Let us try it on some examples.

> f;

> f1:=diff(f,x);

> f2:=int(f1,x);

You see that in this example, I(D(f)) = f.

Is it always true? No.

Here is another example:

> f:=(x+1)^2;

> f1:=diff(f,x);

> f2:=int(f1,x);

And you see that f2 is not equal to f.

The general rule is:

I(D(f)) = f + C,

where C is a constant.

By the way, the indefinite integral of a function is not defined uniquely, but up to an arbitrary additive constant: for example, sin(x) is the integral of cos(x), but it is also true that sin(x)+2 is the integral of cos(x).

Maple command int(f,x) chooses only one function which is the indefinite integral of f.

The property that "int" is inverse to "diff" can serve as the definition of the indefinite integral, while the notion of definite integral is used to construct the indefinite integral.

The indefinite integral of the function f can be constructed as the definite integral with variable upper bound:

> f:='f';

> F(x)=Int(f(t),t=0..x);

To find the value of the function F(x), you have to calculate the definite integral of f(t) from t=0 to t=x. Then, if x changes, F(x) also changes, and we obtain a function x -> F(x). According to the main theorem of calculus ("Newton-Leibnitz theorem"), this function has the property that F'(x) = f(x).

Thus, the relation between derivative and definite integral goes through the indefinite integral:

derivative <--> indefinite integral <--> definite integral

Enough of theoretical review for today.

Now let us do some exercises.

The first series of exercises concerns testing the Maple function int for symbolic integration. Note that, although there is no problem in symbolic differentiation of elementary functions (the derivative of any elementary function is an elementary function that can be found by a simple algorithm), the problem of symbolic integration is quite hard (there are elementary functions whose integral is not elementary, and the corresponding algorithms are not simple).

Exercise 1.

Find the indefinite integrals of the functions (a)--(j) using the Maple function int.

Check each result by the command diff.

a. (x-1)^3

b. e^x/(e^x+1)

c. x*ln(x)

d. tan(x)

e. cos(x)^4

f. x/(x^2+1)^(1/2)

g. x^(-4)/(x^6-1)^(1/2)

h. (6*x^3-19*x^2+23*x-28)/(x^4-4*x^3+3*x^2-16*x+16)

i. (1+x^2)^(-2/3)

j. (1+x^2+x^4)^(3/2)

k. sin(x)/x

The answers that you get in the last three examples (i)--(k) which are not elementary functions, are expressed through so called "special functions": hypergeometric function, elliptic function and "integral sine" Si = int(sin(x)/x,x).

If you find the indefinite integral of a function of several variables, then you must remember that the constant of integration in this case is not just a constant, but a constant that depends on all the remaining variables.

For example, let

> f:=2*x*y;

Then Maple says that the integral over x is:

> f1:=int(f,x);

You can check this as follows:

> diff(f1,x);

But, in fact, you can add any arbitrary function g(y) to f1, you will have the same property:

> diff(f1+sin(y)+1,x);

-- because diff(sin(y)+1,x) = 0.

Exercise 2. Find a function f(x,y) such that

diff(f,x)=y/(x-y)^2

and

diff(f,y)=-x/(x-y)^2.

Exercise 3. Find a function f(x,y,z) such that

diff(f,x) = x^2-y*z,

diff(f,y) = y^2-x*z,

diff(f,z) = z^2-x*y.

Let us now discuss the definite integral and its applications in computing areas and volumes.

Example.

Find the area enclosed by the two lines

y=8/(x^2+4) and y=1.

Solution.

First of all, let us draw the graphs of these two functions and have a look at the area in question:

> plot({8/(x^2+4),1},x=-4..4,scaling=constrained);

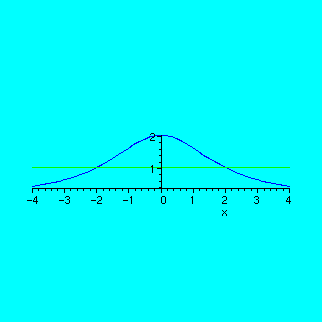
To find the values of x at the two endpoints, solve the system of two equations:

> solve({y=8/(x^2+4),y=1},{x,y});

Now, use definite integral to find the area:

> int(8/(x^2+4)-1,x=-2..2);

Approximate decimal value:

> evalf(%);

In each of the following Exercises 4--7 , find the area of the region bounded by the curves with given equations, following the previous example.

Exercise 4.

y=8*x-x^2, y=2*x

Exercise 5.

y=sin(x)^2, y=0, x=0, x=Pi.

Exercise 6.

x^2*y=4, x=1, x=3, y=0.

Exercise 7.

2*y=x^2, y^2=16*x.

Exercise 8.

Find the area of the circle of radius 1, using definite integral.

Now let us do some exercises on application of definite integrals to the calculation of volumes.

Example.

Find the volume of the ball of radius 1, if you know the formula for the area of the circle S=Pi*R^2.

Solution.

To find the volume of a body, one has to consider the area of the sections by planes z=t from t=t0 to t=t1 (minimal and maximal values) and then integrate this function over t between t0 and t1.

Let us first look at a section of the sphere given by the equation x^2+y^2+z^2=1::

> plot3d({sqrt(1-x^2-y^2),1/2},x=-1..1,y=-1..1,grid=[60,60]);

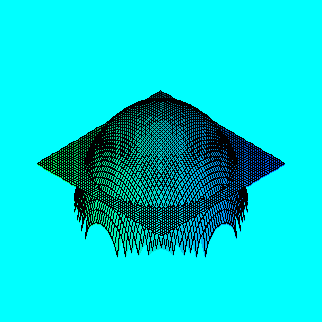
The section by the plane z=t is a circle of radius R=(1-t^2)^(1/2), so its area is

S=Pi*(1-t^2). Therefore, the whole volume is:

> int(Pi*(1-t^2),t=-1..1);

Exercise 9.

Find the volume of the intersection of two cylinders given by the equations x^2+z^2=1, y^2+z^2=1.