4.1 Conditions
Consider the function Pre-alph
, which establishes the relation
of precedence between letters in the standard alphabetical order.
In Chapter 3 we defined it as follows:
Pre-alph {
*1.This relation is reflexive
s1 s1 = T;
*2.If the letters are different, see whether the
* first is before the second in the alphabet
s1 s2 = <Before s1 s2 In <Alphabet>>; }
Before {
s1 s2 In eA s1 eB s2 eC = T;
eZ = F; }
Alphabet { = 'abcdefghijklmnopqrstuvwxyz'; }
This definition is in basic Refal. In full Refal,
function Pre-alph
can be defined without
introducing the auxilliary function Before
:
Pre-alph {
s1 s1 = T;
s1 s2, <Alphabet>: eA s1 eB s2 eC
= T;
e1 = F; }
Here we have used a where-clause which imposes an
additional condition on the applicability of a sentence. The
condition here is:
<Alphabet>: eA s1 eB s2 eC
It follows the left side of a sentence, being separated from it
by the special where-with sign of Refal. In Refal-5 this sign
can be represented either by the ampersand & , or by the comma
,
. It is used to form both where-clauses and with-clauses (blocks).
As we shall see shortly, a with-clause is readily distinguishable
from a where-clause by the presence of braces. Some programmers, however, may
prefer using the comma as the where sign, and the ampersand as the
with sign (or vice versa). In this book we use the comma in both roles.
A condition is a matching pair where the pattern (the right operand)
can be any pattern expression and the argument (the
left operand) can be any Refal expression; the only limitation on the
argument is that it must include only those variables that
have definite values at the moment the condition
is executed ( bound variables). For a condition which immediately
follows the left side
of the sentence, this requirement means that only those variables
which appear in the left side of the sentence can be used in the argument.
The pattern expression in the right side of a condition
can include both bound variables with certain values
and free variables which have not yet been defined and
which get values in the process of matching.
There may be several consecutive where-clauses in a sentence.
The conditions thus introduced will be executed (checked) in sequence.
Let
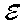 :
:
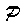 be a condition. It is executed as follows. First,
the Refal machine creates a new view field, puts
be a condition. It is executed as follows. First,
the Refal machine creates a new view field, puts
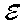 into it, and
replaces the variables in
into it, and
replaces the variables in
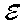 by their values. Then it works, as
usual, on this view field until its content is passive. More
view fields may be created in the process of computation. When
the process is finished, the result is matched to the pattern
by their values. Then it works, as
usual, on this view field until its content is passive. More
view fields may be created in the process of computation. When
the process is finished, the result is matched to the pattern
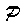 In this matching, those variables of
In this matching, those variables of
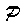 which are already bound
are replaced by their values, while free variables take values in
matching. If the matching succeeds, the next condition
is executed; if there are no further conditions, the replacement
of the left side by the right side takes place.
If the matching fails, a deadlock situation is declared
in the preceding matching (which may be either a condition or
the left side pattern matching). Then
open variables in the pattern will be lengthened as long as possible.
If there are no more open variables to lengthen, the deadlock situation
is carried further backward; if this happens to the left side matching,
the sentence is inapplicable, as in the basic Refal, and the next sentence
is tried. Whether the condition succeeds or fails, the temporary
view field created for
which are already bound
are replaced by their values, while free variables take values in
matching. If the matching succeeds, the next condition
is executed; if there are no further conditions, the replacement
of the left side by the right side takes place.
If the matching fails, a deadlock situation is declared
in the preceding matching (which may be either a condition or
the left side pattern matching). Then
open variables in the pattern will be lengthened as long as possible.
If there are no more open variables to lengthen, the deadlock situation
is carried further backward; if this happens to the left side matching,
the sentence is inapplicable, as in the basic Refal, and the next sentence
is tried. Whether the condition succeeds or fails, the temporary
view field created for
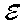 is destroyed, and the Refal machine returns to
the view field from which
is destroyed, and the Refal machine returns to
the view field from which
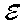 was called.
was called.
Thus each pattern in a sequence of conditions may assign values to new
variables which become bound in subsequent conditions.
In the end, all of these variables will have values and
can be used in the right side.
In the case of Pre-alph
, when the condition is executed, the
value of <Alphabet>
is evaluated. In the matching that follows,
s1
and s2
are replaced by their values, i.e., the letters
to be compared. The matching will succeed if and only if s1
precedes s2
in the alphabet.
The implementation of conditions takes, essentially, the same lines
as the translation of conditions into basic Refal. For each condition
an auxiliary special function is created which executes the matching
required by the condition. These functions have names formed from
the name of the calling function by adding $1, $2, etc.
Suppose we have the call <
F
 >
, such that
in the next step the Refal machine applies one of the
sentences of F which includes a condition:
>
, such that
in the next step the Refal machine applies one of the
sentences of F which includes a condition:
F {...
 ,
, 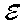 :
: 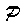 =
=  ;
...
}
;
...
}
Then the system will insert a call of the auxiliary function
F$n between the end of the argument  and the closing activation
bracket:
and the closing activation
bracket:
<F  <F$n
<F$n 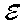 >>
>>
By the general rule, the active subexpressions of 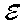 (if any)
will be computed now; then control will pass to F$n.
This function, however, is special; only the matching part of the step
is executed, namely the computed
(if any)
will be computed now; then control will pass to F$n.
This function, however, is special; only the matching part of the step
is executed, namely the computed 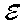 is matched to
is matched to 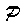 .
Then control is passed back to F. If the match is successful, the
substitution of
.
Then control is passed back to F. If the match is successful, the
substitution of  takes place, otherwise the next sentence is tried.
In any case, the call of F$n, which was earlier inserted,
is removed.
takes place, otherwise the next sentence is tried.
In any case, the call of F$n, which was earlier inserted,
is removed.
This mechanics is useful to know when the tracer is used.
Let us trace the computation of
<Pre-alph 'ba'>
After one step, we shall see in the view-field:
<Pre-alph 'ba'<Pre-alph$1 <Alphabet>>>
Now <Alphabet>
will become active with the result:
<Pre-alph 'ba'<Pre-alph$1 'ab...z'>>
If now we ask the tracer to print the active expression, we shall see
<Pre-alph$1 'ab...z'>
as if Pre-alph$1
were a real function. However, it is the call
of Pre-alph
, not Pre-alph$1
, that will be replaced,
so that after the next step we have:
F
Exercise 4.1
Define a function which looks for the first top-level entry
of an additive operation, i.e., '+'
or '-'
sign, and
encloses the preceding sub-expression in parentheses.
Exercise 4.2
In some releases of the Refal-5 system there is only
whole arithmetic, and the predicate Compare
is not built-in. The predicates to compare whole numbers
can be defined in Refal using subtraction.
Define Less
and Lesseq
( and
and  )
for whole numbers (see Reference Section C
for the formats).
)
for whole numbers (see Reference Section C
for the formats).
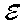 :
:
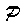 be a condition. It is executed as follows. First,
the Refal machine creates a new view field, puts
be a condition. It is executed as follows. First,
the Refal machine creates a new view field, puts
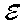 into it, and
replaces the variables in
into it, and
replaces the variables in
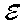 by their values. Then it works, as
usual, on this view field until its content is passive. More
view fields may be created in the process of computation. When
the process is finished, the result is matched to the pattern
by their values. Then it works, as
usual, on this view field until its content is passive. More
view fields may be created in the process of computation. When
the process is finished, the result is matched to the pattern
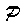 In this matching, those variables of
In this matching, those variables of
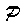 which are already bound
are replaced by their values, while free variables take values in
matching. If the matching succeeds, the next condition
is executed; if there are no further conditions, the replacement
of the left side by the right side takes place.
If the matching fails, a deadlock situation is declared
in the preceding matching (which may be either a condition or
the left side pattern matching). Then
open variables in the pattern will be lengthened as long as possible.
If there are no more open variables to lengthen, the deadlock situation
is carried further backward; if this happens to the left side matching,
the sentence is inapplicable, as in the basic Refal, and the next sentence
is tried. Whether the condition succeeds or fails, the temporary
view field created for
which are already bound
are replaced by their values, while free variables take values in
matching. If the matching succeeds, the next condition
is executed; if there are no further conditions, the replacement
of the left side by the right side takes place.
If the matching fails, a deadlock situation is declared
in the preceding matching (which may be either a condition or
the left side pattern matching). Then
open variables in the pattern will be lengthened as long as possible.
If there are no more open variables to lengthen, the deadlock situation
is carried further backward; if this happens to the left side matching,
the sentence is inapplicable, as in the basic Refal, and the next sentence
is tried. Whether the condition succeeds or fails, the temporary
view field created for
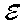 is destroyed, and the Refal machine returns to
the view field from which
is destroyed, and the Refal machine returns to
the view field from which
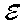 was called.
was called.
 >
, such that
in the next step the Refal machine applies one of the
sentences of F which includes a condition:
>
, such that
in the next step the Refal machine applies one of the
sentences of F which includes a condition:
 ,
,  ;
...
}
;
...
}
 and
and  )
for whole numbers (see Reference Section C
for the formats).
)
for whole numbers (see Reference Section C
for the formats).