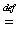Построение множества, заданного рекурсивным определением - на примере программы расстановки ферзей на шахматной доске

А.И. Адамович, А.В. Митин, Р.В. Позлевич

Введение

Пусть P, D-некоторые множества, pP. Рассмотрим задачу построение множества (решений некоторой проблемы) М(p)D , заданного следующим рекурсивным определением:

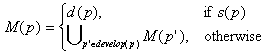
где:

Подобное описание допускают многие задачи из класса "построение множества решений проблемы". В том числе и задачи, связанные с поиском решений на (рекурсивно определяемом) дереве решений:

Данная работа посвящена изучению эффективности реализации задач задач построения множества, заданного рекурсивным определением, в Т-системе [1]-в среде программирования, поддерживающей автоматическое динамическое распараллеливание программ, разработанной в ИЦМС ИПС РАН. Общая проблема в последующем тексте рассматривается на примере реализации программы построения множества всех бесконфликтных) расстановок n ферзей на шахматной доске заданного размера nn.

Задача расстановки ферзей на шахматной доске

Пусть n>1 некоторое число. Рассмотрим бесконфликтную расстановку kn ферзей на шахматной доске размера nn. Из условия бесконфликтности очевидно, что на каждой горизонтали этой доски стоит ровно один ферзь. Занумеруем горизонтали и вертикали доски числами 0..(n-1). Тогда, любая бесконфликтная расстановка может быть записана как массив целых чисел board={v0, v1,... vn-1}, где vh-равно:

Хорошо известная идея решения задачи расстановки ферзей на шахматной доске состоит в следующем: рассмотрим пустую доску {-1, -1,... -1} (она бесконфликтная). Начиная с пустой доски будем последовательно рассматривать все горизонтали h=0,...,n-1 не полностью заполненных бесконфликтных досок и для них рассматривать все варианты бесконфликтного добавления одного ферзя в первую (младшую) из незаполненных горизонталей в них.

Формально это можно записать в виде следующего определения:

Замечание. Так как в параметры (n, h, v) входит номер первой свободной горизонтали в расстановке v можно не требовать, что бы vi==-1 для свободных горизонталей i.

Ниже (Рисунок 1) приведен рекурсивный алгоритм (используется очевидный псевдокод) построения множества всех бесконфликтных расстановок n ферзей на шахматной доске размера nn, адекватный приведенному выше определению множества M(p0).

Реализация Т-программы построения множества всех бесконфликтных расстановок n ферзей на шахматной доске размера nn

При разработке Т-программы на базе рассмотренного алгоритма (Рисунок 1) необходимо принять несколько технических решений: 

main(int n)

{ set Results;
  int board[n];
  Results = M(n,0,board);
}

func M(n,h,board) -> (boards)     // результат -- множество полных бесконфликтных
  int  v;                         // расстановок, получаемых дозаполнением board
  *int board1;
  set  Sum;                       // Sum -- "сумматор" для результата
                                  //*********************************************
                                  // Eсли board - полная расстановка, то 
  if (n==h) return board;       // результат--множество из одного элемента --
                                  // board
                                  //*********************************************
                                  // Eсли board - не полная расстановка, то 
  Sum = ;	                      // h<n - очередная пустая горизонталь.
  for (v=0; v<n; v++)             // Перебираем все вертикали v такие, что
    if (no_conflict(board,h,v) {  // в позиция (h,v) расстановки board можно
                                  // бесконфликтно поставить ферзя. Для них:
       board1 = new_copy(desc,n); //    создаем board1 - копию board
       board1[h] = v;             //    ставим ферзя в (h,v) на board1

       Sum = SumM(n,h+1,board1);	//    добавляем к Sum все дозаполнения board1

    }                             // В конце перебора всех вертикалей, Sum и 

  return Sum;                     // есть множество всех полных бескон-
                                  // фликтных расстановок, получаемых дозапол-
                                  // нением board
}

func no_conflict (board,hq, vq)  (boolean) 
// Предикат: можно ли в расстановке board, в первую пустуя горизонталь hq (все
// ферзи выше hq) бесконфликтно поставить одного ферзя в позиции (hq,vq)

   int h, v;
   for(h = 0; h < hq; h++) {     // Перебираем все позиция (h,q) уже расставлен-
      v = board[h];              // ных ферзей. Если ферзь (h,q) бьет (hq,vq):
      if (     vq == v           //   по вертикали
            || (vq-hq) == (v-h)  //   или диагонали +45 град;
            || (vq+hq) == (v+h)  //   или диагонали -45 град
         )                       // то предикат ложен.
         return (FALSE);         // 
   }                             // Если перебрали всех расставленных ферзей и
   return (TRUE);                // ни один из них не бил (hq,vq), то предикат 
}                                // истинен
Рисунок
1.  Алгоритм построения множества всех бесконфликтных расстановок
n ферзей на шахматной доске заданного размера nn

В сети Интернет по адресу:

ftp://ftp.botik.ru/pub/local/Sergei.Abramov/T-system/

доступен полный текст t2cp-программы q7_fl_gc построения множества всех бесконфликтных расстановок n ферзей на шахматной доске размера nn, в которой:

Опишем состав Т-программы:

  • Результат функции queens-дерево, листьями которого являются L-пакеты, содержащие в совокупности все возможные полные бесконфликтные расстановки, полученные дозаполнением расстановки b. Для построения такого дерева в функции queens выполняется следующее:
    • Если hq >= (N0`int) то:
      • за счет рекурсии Си-функции (без порождения новых Т-процессов) функции complete_desk_b_and_add_results_to_bs строится лисп-список bs всех возможных полных бесконфликтных расстановок, полученных дозаполнением расстановки b;
      • Си-функцией pack_bs лисп-список преобразуется в L-пакет pbs;
      • L-пакет pbs выдается в качестве результата pboards_tree функции queens (дерево-лист).
    • Если hq < (N0`int) то:
      • В итерации (vq = 0 n-1) ищутся все такие номера вертикали vq, то в заполнение b можно бесконфликтно добавить ферзя в позицию (hq, vq).
      • Для всех таких vq рекурсивно вызывается Т-функция
        queens(bnew,h1,N,N0)
        где h1`int=h`int+1, bnew-расстановка, полученная копированием расстановки b и добавлением в нее одного ферзя в позицию (hq, vq). Результаты (деревья L-пакетов решений) всех вызванных Т-функций сохраняются в элементах Т-списка branch:
        `[ branch`list[nbrs] ] = queens(bnew, h, N, N0);
        nbrs++;
      • Построенный T-список branch деревьев L-пакетов решений преобразуется в развилку дерева-branch`mark_as_branch-и выдается в качестве результата pboards_tree функции queens (дерево-развилка).

    • Результаты исполнения в Т-системе программы q7_fl_gc построения множества всех бесконфликтных расстановок n ферзей на шахматной доске размера nn

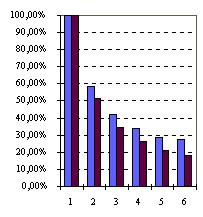
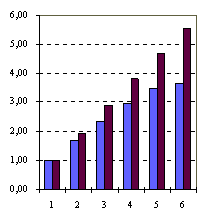
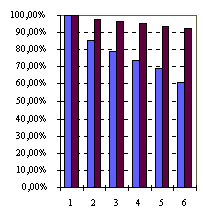
    Ниже (Таблица 1, Рисунок 2) приведены сведения о результатах исполнения Т-программы q7_fl_gc под управлением Т-системы:

    Видно, что Т-система поддерживает удовлетворительную эффективность автоматического распараллеливания Т-программы q7_fl_gc в случае взаимодействия соисполнителей по протоколу IP и высокую-в случае SMP. Значительное превосходство варианта SMP над вариантом LAN связано с тем, что по природе задачи мы имеем дело с большим объемом генерируемых данных (по сравнению с объемом вычислений). Таким образом, в общее реальное (астрономическое) время выполнения задачи складывается из (а) собственно времени счета и (б) времени сборки и вывода достаточно объемного результата (365,596145 Мбайт-объем внутреннего представления, 17 Мбайт-объем вывода в текстовый файл). Если первое слагаемое (а) можно уменьшать за счет параллельного исполнения, то второе (б) остается практически постоянным. Использование вариантом LAN для передач данных сетевого протокола IP приводит к высоким затратам на эти передачи и, как следствие-к снижению утилизации вычислительной мощности.

    Таблица 1. Результаты исполнения Т-программы q7_fl_gc под управлением Т-системы
    число про-
    время счета
    (сек)
    время счета
    (%)
    коэффициент ускорения
    утилизация вычислительной мощности
    цессо-ров
    LAN
    SMP
    LAN
    SMP
    LAN
    SMP
    LAN
    SMP
    1
    		194 193100,00%100,00% 1,001,00100,00% 100,00%
    2
    		113 9958,42%51,07% 1,711,9685,58% 97,90%
    3
    		82 6742,27%34,62% 2,372,8978,87% 96,29%
    4
    		66 5134,04%26,27% 2,943,8173,45% 95,16%
    5
    		56 4128,88%21,38% 3,464,6869,26% 93,54%
    6
    		53 3527,41%18,04% 3,655,5460,81% 92,38%


    Время счета (%)
    Коэффициент
    ускорения
    Утилизация
    вычислительной
    мощности

    Рисунок 2. Результаты исполнения Т-программы q7_fl_gc под управлением Т-системы

    Список литературы

     

    1999 © T-System© ИЦМС ИПС РАН