Фильтрация потока данных - на примере программы построения списка простых чисел методом "решето Эратосфена"

1998 г. А.И. Адамович, А.В. Митин, Р.В. Позлевич

---

• Введение
• Первый вариант Т-программы.
  • Результаты исполнения
• Улучшенный вариант Т-программы.
  • Результаты исполнения
• Заключение
• Список литературы

---

Введение

Одной из задач с неявным параллелизмом является задача фильтрации потока. Рассмотрим следующую формулировку данной задачи. Пусть дано множество (представленное потоком) некоторых элементов ns1 = [n1, n2, ] и задано некоторое отношение (_._), по которому следует отфильтровать данный поток, в соответствии со следующей процедурой:

1. Выберем (и удалим) первый элемент p1=head(ns1) из потока ns1. Оставшиеся в потоке tail(ns1) элементы отфильтруем при помощи предиката del1(x) = (xp1). Отфильтрованный поток обозначим:
   ns2 = [ n | n   tail(ns1), (n p1) ].
2. Выберем (и удалим) первый элемент p2=head(ns2) из потока ns2. Оставшиеся в потоке tail(ns2) элементы отфильтруем при помощи предиката del2(x) = (xp2). Отфильтрованный поток обозначим:
   ns3 = [ n | n   tail(ns2), (n p2) ].
3. И так далее, до тех пор, пока очередной поток nsk не окажется пустым.
4. Найденный поток элементов ps = [p1, p2, pk] являются результатом фильтрации исходного потока ns1 по отношению (__).

Приведем несколько примеров задач, относящихся к данному классу:

• Если рассматривать:
  • в качестве элементов-натуральные числа;
  • в качестве отношения (ab)-делимость нацело числа a на b (в Си-нотации: a%b==0);
  • в качестве входного потока-поток ns1 = [2, 3, 4, ,N];

то общая задача совпадет с построением при помощи алгоритма "решето Эратосфена" таблицы ps = [p1, p2, pk] всех простых чисел из отрезка [2..N].

• Если в качестве отношения (__) рассматривается произвольное отношение эквивалентности над элементами ns1, то результатом фильтрации является множество всех представителей (попарно неэквивалентных друг другу) ps = [p1, p2,   pk], определяющих фактор-множество от ns1 по (__).

Данная работа посвящена изучению эффективности реализации задач фильтрации потока данных в Т-системе [1]-в среде программирования, поддерживающей автоматическое динамическое распараллеливание программ, разработанной в ИЦМС ИПС РАН. Общая проблема в последующем тексте рассматривается на примере реализации программы построения списка простых чисел методом "решето Эратосфена".

Первый вариант реализации Т-программы алгоритма "решето Эратосфена"

В разделе 2.1 приведен результат прямого (наивного) описания алгоритма "решето Эратосфена" на языке t2cp [1]. Программа состоит из следующих фрагментов:

• nats(n) -> (ns) -потоковая Т-функция, определяет ленивый поток натуральных чисел [2,3,... n'int].
• filter(a, ns) -> (fs) -потоковая Т-функция, реализует отдельный фильтр-из потока ns удаляются все элементы n, которые делятся на a, оставшиеся элементы составляют результат-поток fs.
• sieve(ns) -> (ps) -потоковая Т-функция, реализует собственно алгоритм "решето Эратосфена": из потока ns берется первое число ns`head и отсылается в поток результатов ps, а на оставшиеся элементы ns`tail запускается отдельный фильтр:
  

`[ns] = filter(ns`head, ns`tail).

Данное действие выполняется до тех пор пока поток ns не станет пустым.

• tmain(arg) -> (rc) -главная Т-функция Т-задачи, принимает параметры командной строки, за счет вызовов функций nats и sieve определяет поток ps простых чисел и выполняет печать простых чисел в файл.
• Вспомогательные Си-функции check_arg и _ut_app_init_step реализуют проверку корректности параметров командной строки.

Ниже (см. Рисунок 1) представлен возможный процесс развития вычисления рассматриваемой Т-программы.

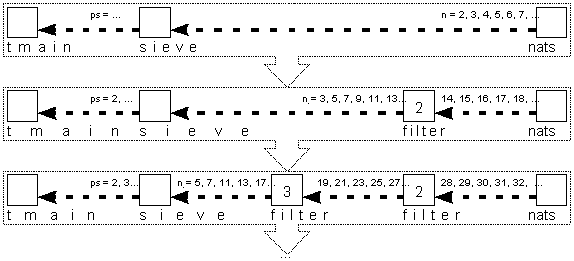
Рисунок 1. Возможный процесс развития вычисления Т-программы "решето Эратосфена"

Т-программа наивной реализации алгоритма "решето Эратосфена"

#include <stdio.h>

#include <stdlib.h>

#include <ctype.h>

#include "t2cp.h"

#define FALSE 0

#define TRUE 1

#define AUTOWAIT TRUE

#define DATACHECK TRUE

FILE * fp_res;

/* nats(n) -- ленивый поток натуральных чисел 2,3,...,n'int */

`func nats(n) -> (ns) stack (512) lazy stream;

int i, i_lim = n`int;

for(i=2; i<=i_lim; i++) {

n`int = i;

(n)`streamsend(ns);

}

n`mkNil;

`ns <== n;

`end_func

/* решето Эратосфена */

`func sieve(ns) -> (ps) stack (512) stream;

while( ! ns`isNil ) {

(ns`head)`streamsend(ps);

`[ns] = filter(ns`head, ns`tail);

}

/* здесь ns == NIL */

`ps <== ns;

`end_func

/* отдельный фильтр filter(a, ns) -> (fs) -- из потока ns оставляет

те элементы fs, которые не деляться на a */

`func filter(a, ns) -> (fs) stack (512) stream;

int i_a = a`int;

while( ! ns`isNil ) {

if ( ( ns`head`int % i_a ) != 0) {

(ns`head)`streamsend(fs);

}

`ns = ns`tail;

}

/* здесь ns == NIL */

`fs <== ns;

`end_func

`func tmain(arg) -> (rc) ;
`vars ps, N;

   int n = atoi( (arg`list[0])`packed_ptr(char) ), /* макс. число в потоке  */
       nres = 0;                                   /* счетчик простых чисел */

   N`mkInt( n );                       /* макс. число в исходном потоке */
  `[ps] = nats(N);                     /* поток натуральных [2..N]      */
  `[ps] = sieve(ps);                   /* поток простых из [2..N]       */

   /* Печать списка простых чисел */
   while ( ! ps`isNil ) {
      fprintf (fp_res, "%d\n", (ps`head`int));
      nres++;
     `ps = ps`tail;
   }
   printf ("End list of %d results\n", nres);
   fflush (stdout);
   fclose (fp_res);

   N`mkInt(0);
  `rc <== N;
`end_func

Результаты исполнения в Т-системе наивной реализации алгоритма "решето Эратосфена"

Простейший анализ приведенной выше t2cp-программы позволяет заметить серьезный недостаток-гранула параллелизма имеет малую вычислительную сложность. Очень маленьким-буквально десяток команд-является и цикл байта для гранул параллелизма (среднее число операций на каждый введенный-или выведенный-в гранулу параллелизма байт).

Как результат, мы получаем не уменьшение, а существенное увеличение времени счета задачи при переходе от однопроцессорной аппаратуры к многопроцессорной. Так например, при параметре N=10000 на однопроцессорной установке (Pentium Pro 200) под управлением Т-системы данная программа построила 1229 простых числа из отрезка [2...10000] за 9.53 сек. А на двухпроцессорной установке та же задача и с теми же параметрами исполнялась 265.33 сек. (замедление в 28 раз)!

Этот "результат" иллюстрирует тот факт, что при создании Т-программ программист должен уделять достаточное внимание анализу характеристик гранул параллелизма и если нужно, идти на изменение алгоритма, чтобы улучшить эти характеристики.

Чудес не бывает, и слова "Т-система реализует концепцию автоматического динамического распараллеливания программ" не означают, что программист вовсе освобожден от необходимости продумывать свой код. Как и в любой системе (среде) программирования, в Т-системе программист обязан думать при проектировании программы о выполнении тех необходимых условий получения эффективного кода, которые предъявляются особенностями используемой аппаратно-программной среды (платформы). Для Т-системы таким важнейшими условиями, от исполнения которых напрямую зависит качество распараллеливания программ (во время их исполнения в Т-системе), является требования на характеристики определенных программистом гранул параллелизма.

Улучшенный вариант Т-программы алгоритма "решето Эратосфена"

В данном разделе описана модификация наивной реализации t2cp-программы алгоритма "решето Эратосфена", существенно улучшающая характеристики гранул параллелизма.

Терминология и структуры данных. L-пакеты

Пакетом с длиной (L-пакетом) будем называть звено-держатель xp упакованного Си-массива, содержащего несколько (L_xp) целых чисел x1,...,xL_xp, расположенных в xp следующим образом:

   xp'packed_ptr(int) [0]    = L_xp // длина
   xp'packed_ptr(int) [1]    = x1
   xp'packed_ptr(int) [2]    = x2
   ...
   xp'packed_ptr(int) [L_xp] = xL_xp

Если звено xp-L-пакет, то будем также называть L-пакетом Си- указатель:

int * x = xp'packed_ptr(int);

   x[0]     = L_xp -- длина
   x[1]     = x1
   x[2]     = x2
   .
   x[L_xp]  = xL_xp

1. Описание программы

Основой идей улучшения характеристик гранул параллелизма в рассматриваемой задаче является:

• переход от использования потоков одиночных данных (потоков отдельных натуральных чисел) к потокам L-пакетов натуральных чисел;
• использование пакетных генератора и фильтров.

Пакетный генератор. Генератор nats(n, npMax) -> (nps) -создает ленивый поток L-пакетов натуральных чисел: 2,3,...,n'int. Каждый пакет np в потоке nps содержит не более (последний пакет может быть коротким) npMax'int чисел.

Пакетный фильтр. Фильтр filter(pp, nps, npMax) -> (fps) - при помощи набора (L-пакета) простых чисел pp фильтрует L-пакеты np из потока nps в L-пакеты fp потока fps:

1. Каждый входной пакет np из потока nps распаковываются и каждое число npi из np фильтруется всеми простыми из L-пакета pp:
   1. Если npi делится на некоторое простое из pp, то оно отсеивается.
   2. Если npi не делится ни на какое простое из pp, то оно помещается в L-пакет fp (вначале пустой).
2. Когда fp достигнет длины npMax'int, fp направляется в выходной поток fps (при этом заводится следующий пустой L-пакет fp, в который можно разместить до npMax'int следующих чисел).
3. В конце (по исчерпанию потока nps), последний локальный L-пакет fp так же выдается в поток fps (конечно, если fp не пустой). Таким образом, все выдаваемые из фильтра пакеты fp (кроме последнего) имеют длину npMax'int (последний может быть короче).

Решето Эратосфена. Решето sieve(nps,ppMax,npMax) -> (pps):

1. имеет локальный L-пакет pp найденных простых (в начале-пустой);
2. получает поток nps L-пакетов np натуральных чисел (известно, что длина поступающих L-пакетов не более npMax'int);
3. разбирает поток L-пакетов целых чисел-каждое число npi из очередного пакета фильтруется локальным L-пакетом pp-если оно проходит проверку (npi не делится ни на какое число из pp), то npi-простое число, оно добавляется к pp;
4. когда завершается разбор очередного входного пакета np, то выполняет проверку длины локального L-пакетa pp и если он стал длиннее ppMax`int, то:
   1. порождает на потоке nps новый фильтр: [nps] = filter(pp, nps);
   2. выдает pp в поток результатов;
   3. заводит следующий пустой L-пакет pp, в который можно разместить до npMax'int+ppMax'int чисел;
5. в конце работы (по исчерпанию потока nps), последний локальный L-пакет pp найденных простых так же выдается в поток результатов (конечно, если pp не пустой).

Решение задачи (главная функция). Использую описанные выше функции можно следующим образом построить поток pps L-пакетов всех простых чисел от 2 до N'int:

      [nps] = nats(N, npMax); 
      [pps]  = sieve(nps, ppMax, npMax)

где npMax'int, ppMax'int -любые числа, большие 1.

Параметры npMax'int, ppMax'int определяют характеристики гранул данных (что передается в потоках между процессами) и гранул вычислений, соответственно. Задавая различные значения этих параметров можно регулировать:

• общую вычислительную сложность гранул параллелизма-в среднем для процессов filter выполняется около npMax'int*(npMax'int/2+ppMax'int) операций делений на каждый введенный из входного потока пакет;
• цикл байта для гранул параллелизма (среднее число операций на каждый введенный или выведенный байт)-в среднем для процессов filter выполняется около npMax'int/8 + ppMax'int/4 операций делений на каждый введенный байт.

Параметры командной строки. В качестве параметров командной строки для улучшенной t2cp-программы алгоритма "решето Эратосфена" задаются три натуральных числа:

• N`int >2 -предельное (максимальное) число-простые числа будут отбираться из отрезка [2..N`int];
• ppMax`int >2 -ограничение на размер пакета pp простых чисел;
• npMax`int >2 -ограничение на размер пакета np фильтруемого потока.

Структура программы. Полный текст t2cp-программы улучшенной реализации алгоритма "решето Эратосфена" доступен в сети Интернет по адресу:

ftp://ftp.botik.ru/pub/local/Sergei.Abramov/T-system/

Основные фрагменты данной программы:

• nats(n,npMax) -> (nps) -потоковая Т-функция, пакетный генератор потока целых из отрезка [2..N`int];
• static inline int chk_filter (int a, int* pp) -Си-функция-предикат, проверка неделимости числа a на все числа L-пакета int* pp;
• sieve(nps,ppMax,npMax) -> (pps) -потоковая Т-функция, решето Эратосфена;
• filter(pp, nps, npMax) -> (fps) -потоковая Т-функция, пакетный фильтр;
• tmain(arg) -> (rc) -главная Т-функция Т-задачи, принимает параметры командной строки, за счет вызовов функций nats и sieve определяет поток pps L-пакетов простых чисел и выполняет печать простых чисел в файл.
• Вспомогательные Си-функции check_arg и _ut_app_init_step реализуют проверку корректности параметров командной строки.

Результаты исполнения в Т-системе улучшенной реализации алгоритма "решето Эратосфена"

Ниже (Таблица 1, Рисунок 2) приведены сведения о результатах исполнения Т-программы f4_epfgs.tlc под управлением Т-системы:

Программа выполнялась для следующих значений параметров командной строки:

• N`int = 2 500 000 -предельное (максимальное) число, поиск простых чисел выполнялся в отрезке [2..2 500 000];
• ppMax`int = 1000 -ограничение на размер пакета pp простых чисел;
• npMax`int = 1000 -ограничение на размер пакета np фильтруемого потока.

Таким образом, генерируемый поток содержал 2500 пакетов по 1000 чисел в каждом. Результат фильтрации-183072 простых чисел (количество пакетов-184).

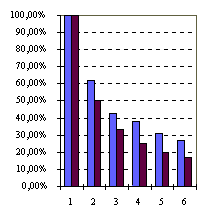
Вычисления проводились на ЭВМ ALR 6x6. За счет конфигурирования Т-системы для решения задачи использовалось различное число процессоров установки (от 1 до 6) и различные способы организации взаимодействия отдельных соисполнителей-несколько (от 1 до 6) соисполнителей, взаимодействие через протокол IP (далее обозначается как LAN) и один соисполнитель, способный использовать от 1 до 6 процессоров-общая память (SMP). При каждом запуске (на разном числе процессоров) использовался один и тот же исполняемый код задачи и одни и те же параметры входной строки.

Таблица 1. Результаты исполнения Т-программы f4_epfgs под управлением Т-системы

число про-	время счета (сек)		время счета (%)		коэффициент ускорения		утилизация вычислительной мощности
цессо-ров	LAN	SMP	LAN	SMP	LAN	SMP	LAN	SMP
1	3 034	3 033	100,00%	100,00%	1,00	1,00	100,00%	100,00%
2	1 866	1 521	61,50%	50,14%	1,63	1,99	81,30%	99,73%
3	1 310	1 015	43,16%	33,45%	2,32	2,99	77,23%	99,64%
4	1 155	762	38,05%	25,12%	2,63	3,98	65,71%	99,51%
5	938	610	30,90%	20,12%	3,24	4,97	64,72%	99,40%
6	814	511	26,82%	16,84%	3,73	5,94	62,15%	98,96%

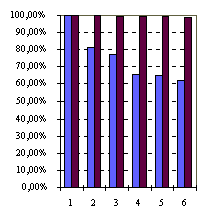
Время счета (%)	Коэффициент ускорения	Утилизация вычислительной мощности

Рисунок 2. Результаты исполнения Т-программы f4_epfgs под управлением Т-системы

Заключение

Из результатов экспериментов можно заметить, что SMP-вариант Т-системы поддерживает высокую, а вариант LAN-удовлетворительную эффективность автоматического распараллеливания Т-программы f4_epfgs.tlc. Недостаточно высокие значения показателя утилизации вычислительный мощности вариантом LAN-по сравнению с SMP-связаны с тем, что по природе задачи фильтрации имеется достаточно большой линейный поток данных, на который "нанизываются" динамически порождаемые процессы. Таким образом, по самой природе задачи объем передач между процессами, расположенными в различных экземплярах Т-системы достаточно велик. А суммарный объем передач между соисполнителями может достигать (Рисунок 3) произведения объема исходного потока на количество обрабатывающих его процессов. При использовании протокола IP это ведет приводит к высоким суммарным затратам на эти передачи. В SMP-варианте аналогичный недостаток отсутствует.

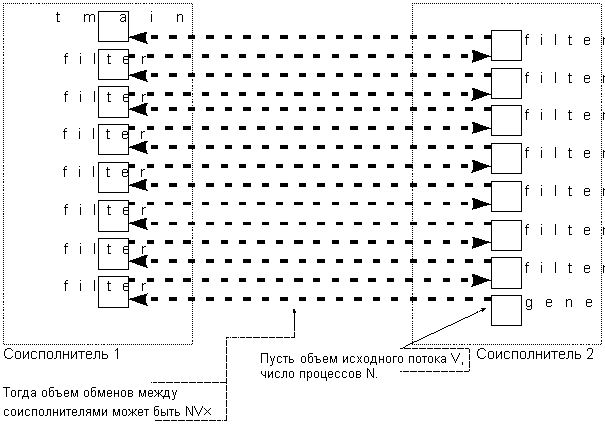
Рисунок 3. Оценка сверху суммарного объема передач между соисполнителями (класс задач: линейный поток данных, на который "нанизываются" динамически порождаемые процессы)

Список литературы

• С.М. Абрамов, А.И. Адамович. Т-система-среда программирования с поддержкой автоматического динамического распараллеливания программ//Принято к печати в: Юбилейный сборник трудов Института программных систем. Под ред. проф. В.И. Гурмана, Переславль-Залесский, ИПС РАН, 1999 г.

 

---