Аннотация: Пусть
![$a(x)\in C^\infty[0,h]$ $a(x)\in C^\infty[0,h]$](img3.gif) ,
,
![$b(x)\in C^\infty[-h,0]$ $b(x)\in C^\infty[-h,0]$](img4.gif) ,
,
 , – действительные функции, не имеющие нулей на обозначенных отрезках. Зафиксируем числа
, – действительные функции, не имеющие нулей на обозначенных отрезках. Зафиксируем числа  ,
,  и рассмотрим дифференциальные выражения (ДВ)
и рассмотрим дифференциальные выражения (ДВ)
Матем. сб., 194 (2003), 5, 109-138.
Условие непроницаемости точки вырождения одночленного
симметрического дифференциального оператора четного порядка
Ю. Б. Орочко
Московский государственный институт электроники и математики
Аннотация:
Пусть
![$a(x)\in C^\infty[0,h]$ $a(x)\in C^\infty[0,h]$](img3.gif) ,
,
![$b(x)\in C^\infty[-h,0]$ $b(x)\in C^\infty[-h,0]$](img4.gif) ,
,
 , – действительные функции, не имеющие нулей на обозначенных отрезках. Зафиксируем числа
, – действительные функции, не имеющие нулей на обозначенных отрезках. Зафиксируем числа  ,
,  и рассмотрим дифференциальные выражения (ДВ)
и рассмотрим дифференциальные выражения (ДВ)
&=(-1)^n(x^pa(x)f^{(n)})^{(n)}(x)...
...
s_q^-[f](x)&=(-1)^n((-x)^qb(x)f^{(n)})^{(n)}(x)
\end{aligned}
\end{equation*} \begin{equation*}
\begin{aligned}
s_p^+[f](x)&=(-1)^n(x^pa(x)f^{(n)})^{(n)}(x)...
...
s_q^-[f](x)&=(-1)^n((-x)^qb(x)f^{(n)})^{(n)}(x)
\end{aligned}
\end{equation*}](img8.gif)
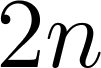 , вырождающиеся в точке
, вырождающиеся в точке
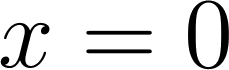 . Через
. Через 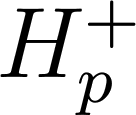 и
и 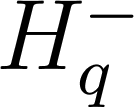 обозначим симметрические
минимальные операторы, порожденные
обозначим симметрические
минимальные операторы, порожденные
$ $s_p^+[f](x)$](img13.gif) и
и
$ $s_q^-[f](x)$](img14.gif) соответственно в гильбертовых пространствах
соответственно в гильбертовых пространствах
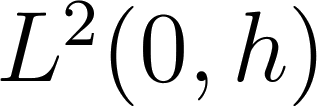 и
и 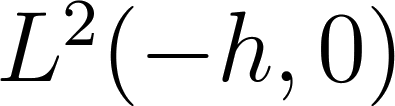 .
.
”Сшивая” ДВ
$ $s_p^+[f](x)$](img13.gif) и
и
$ $s_q^-[f](x)$](img14.gif) в точке
в точке 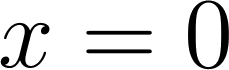 ,
мы получаем новое ДВ
,
мы получаем новое ДВ
$ $s_{pq}[f](x)$](img17.gif) ,
,
![$x\in[-h,h]$ $x\in[-h,h]$](img18.gif) ,
вырождающееся в указанной внутренней точке отрезка
,
вырождающееся в указанной внутренней точке отрезка
![$[-h,h]$ $[-h,h]$](img19.gif) . При определенных ограничениях на
. При определенных ограничениях на 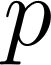 и
и 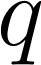 ДВ
ДВ
$ $s_{pq}[f](x)$](img17.gif) порождает симметрический минимальный
оператор
порождает симметрический минимальный
оператор 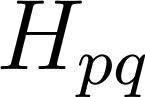 , действующий в
, действующий в 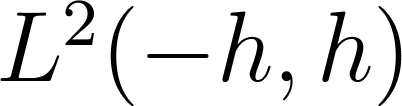 и являющийся
симметрическим расширением ортогональной суммы операторов
и являющийся
симметрическим расширением ортогональной суммы операторов
 . Мы называем точку
. Мы называем точку 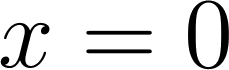 внутренним барьером для ДВ
внутренним барьером для ДВ
$ $s_{pq}[f](x)$](img17.gif) и находим условия, при которых справедливо равенство
и находим условия, при которых справедливо равенство
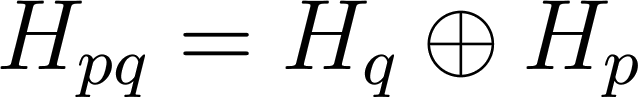 . Естественно назвать такой
внутренний барьер непроницаемым внутренним
препятствием, если это равенство имеет место, и проницаемым внутренним препятствием, если оно
несправедливо. Основной результат данной статьи состоит в том, что точка
. Естественно назвать такой
внутренний барьер непроницаемым внутренним
препятствием, если это равенство имеет место, и проницаемым внутренним препятствием, если оно
несправедливо. Основной результат данной статьи состоит в том, что точка 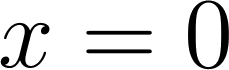 – непроницаемое внутреннее
препятствие, если
– непроницаемое внутреннее
препятствие, если
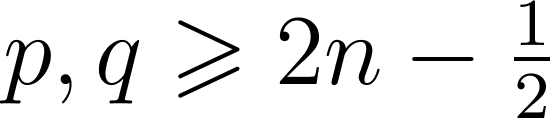 , причем этот
результат является, в определенном смысле, точным.
, причем этот
результат является, в определенном смысле, точным.
Библиография: 8 названий.