 |
T-system: Programming environment |
 |
|
T-system: Programming environment |
|
| Sergei Abramov abram@botik.ru |
Alexey Adamovich lexa@adam.botik.ru |
Maxim Kovalenko mk@adam.botik.ru |
| tel: +7(08535)98.031 | fax: +7(08535)20.593 | fax: +7(08535)98.278 |
1. Introduction |
So far, the problem of implementation of parallel computations is mostly a problem of software rather than hardware.
This paper introduces a software system for automatic dynamic parallelizing of programs developed in RCMS of PSI RAS-the T-system. An example of application of T-system to a task of image rendering using the ray tracing method is also presented.
2. Computation model |
We implement automatic dynamic parallelizing using a new model of organization of the process of computation:
[x,y,z] = G(a,b);
from a process evaluating some other function F has non-standard semantics (is carried out as a network function call).
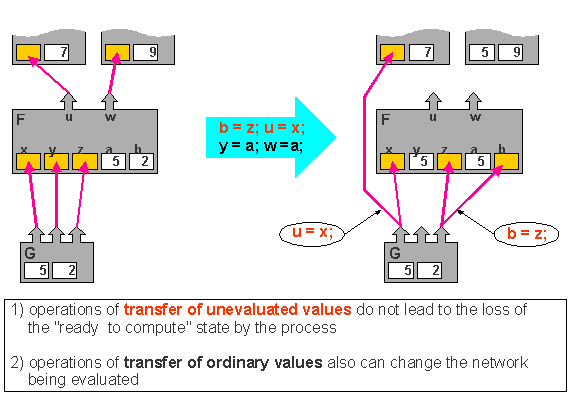
Autotransformation of an network being computed, as a model of organization of computations, opens an opportunity for automatic dynamic parallelizing of programs: for the majority of the applications the organization of the computation in this way provides sufficient number of processes ready to run, and they can be run in parallel.
The model provides the only mechanism of synchronization of processes---the mechanism of suspending and resuming described above.
The closest analogues to our approach are the Daisy/DSI project (Indiana Univ.), the reduction machine, and the MDA system (multiprocessor with dynamic architecture, Russia, 1978-1985 years).
3. T-system |
The T-system is a software environment intended to implement the computation model described in the previous section on a multiprocessor platform.
3.1. Hardware/software platform for T-system |
The current implementation of T-system runs on a "multicomputer" that is a TCP/IP network of IBM/PC clones running OS Linux.
The nearest development plans include:
The main function of T-system is the support of the computation model "autotransformation of evaluation network." Within the framework of this function T-system implements the following basic data structures and operations:
Each processor element of a multicomputer runs its own instance of T-system---the so-called co-executive. The user task is running under the management and with the support of all co-executives.
Functions of T-system related to utilization of all the computational power of a multiprocessor:
Today, the following technique is used for programming applications under T-system: the programs are developed in the C language using a library of functions providing an interface to the T-system kernel. The library provides the programmer with all operations necessary for the considered computation model.
The nearest development plans include:
4. Rendering of the 3-D scene images using T-system |
We have chosen the problem of 3-D scene rendering using ray tracing as the real problem for demonstration of the automatic dynamic parallelizing abilities.
The following algorithm is used at the top level of the program:
[image] main(scene, full_screen_description) {
[tree] = render_scene(scene, full_screen_description);
[image] = flatten(tree);
}
[image_tree] render_scene(scene, part_of_screen_description) {
var part1, part2, tree, part_of_img;
if (size_too_big(part_of_screen_description)) {
[part1,part2] = split(part_of_screen_description);
br_node = new(2);
[br_node[0]] = render_scene(scene,part1);
[br_node[1]] = render_scene(scene,part2);
[image_tree] = br_node; // branch in a tree of image fragments
} else {
... allocation of an array part_of_image and filling it by usual
ray tracing algorithm
image_tree = part_of_image; // leaf in a tree of image
// fragments
}
}
[image] flatten(tree) {
... recursive traversal of the tree and composing
the whole image from its fragments.
}
Pay attention to the fact that the information about the number of co-executives, and the sort of hardware (topology of the network, etc.) is not used in the program. This is one of the main properties of our approach:
The T-program of ray tracing was run on multicomputers consisting of
one, two, three and four personal computers (IBM PC Pentium 166/32Mb/4Gb).
We rendered the images of scenes of various complexities.
The experiments show that T-system supports high
level of utilization of the multiprocessor's computational power
and low level of overhead.
 |
 |
 |
| Scene B2 (3 lights, 91 spheres, 1 polygon) |
Scene G (5 lights, 147 polygons) |
Scene B3 (3 lights, 820 spheres, 1 polygon) |
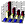Computing time in seconds |
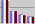Computing time reduction |
||||||
| number of processors | scene B2 | scene B3 | scene G | number of processors | scene B2 | scene B3 | scene G |
| 1 | 278.1 | 2,785.9 | 1,295.2 | 1 | 100.0% | 100.0% | 100.0% |
| 2 | 148.0 | 1,443.5 | 671.9 | 2 | 53.2% | 51.8% | 51.8% |
| 3 | 100.0 | 976.8 | 450.4 | 3 | 35.9% | 35.0% | 34.7% |
| 4 | 77.9 | 747.6 | 345.6 | 4 | 28.0% | 26.8% | 26.6% |
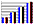Speedup factor |
Computational power utilization |
||||||
| number of processors | scene B2 | scene B3 | scene G | number of processors | scene B2 | scene B3 | scene G |
| 1 | 1.00 | 1.00 | 1.00 | 1 | 100.0% | 100.0% | 100.0% |
| 2 | 1.88 | 1.93 | 1.93 | 2 | 93.9% | 96.5% | 96.3% |
| 3 | 2.78 | 2.85 | 2.88 | 3 | 92.6% | 95.0% | 95.8% |
| 4 | 3.57 | 3.73 | 3.75 | 4 | 89.2% | 93.1% | 93.6% |
 |
 |
| Scene B4 (3 lights, 3781 spheres, 1 polygon) |
Scene G2 (5 lights, 1169 polygons) |
5. Invitation to collaboration |
We are ready to discuss any forms of collaboration with those interested in:
6. Selected publications on T-system |
Most of the publications are FTP-available from Web-page: http://www.botik.ru/~abram/ts-pubs.html.